A Direct Formulation of Sparse PCA using Semidefinite Programming

Download: .pdf

Authors: A. d'Aspremont, L. El Ghaoui, M. Jordan, and G. Lanckriet.

Status: SIAM Review, vol. 49, no. 3, 2007.

Abstract: Given a covariance matrix, we consider the problem of maximizing the variance explained by a particular linear combination of the input variables while constraining the number of nonzero coefficients in this combination. This problem arises in the decomposition of a covariance matrix into sparse factors or sparse PCA, and has wide applications ranging from biology to finance. We use a modification of the classical variational representation of the largest eigenvalue of a symmetric matrix, where cardinality is constrained, and derive a semidefinite programming based relaxation for our problem. We also discuss Nesterov's smooth minimization technique applied to the semidefinite program arising in the semidefinite relaxation of the sparse PCA problem. The method has complexity 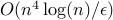, where 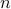is the size of the underlying covariance matrix, and is the desired absolute accuracy on the optimal value of the problem.

Related entries:

• A. d'Aspremont, , L. El Ghaoui, M. Jordan, and G. Lanckriet. A Direct Formulation of Sparse PCA using Semidefinite Programming, Proc. NIPS, 2005.

• Preprint on arXiv.

Code: DSPCA.

Bibtex reference: