On the Quality of a Semidefinite Programming Bound for Sparse Principal Component Analysis

Download: http://arxiv.org/abs/math/0601448.

Author: L. El Ghaoui.

Status: Preprint on arXiv.

Abstract: We examine the problem of approximating a positive, semidefinite matrix 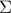by a dyad 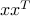, with a penalty on the cardinality of the vector 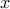. This problem arises in sparse principal component analysis, where a decomposition of 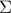involving sparse factors is sought. We express this hard, combinatorial problem as a maximum eigenvalue problem, in which we seek to maximize, over a box, the largest eigenvalue of a symmetric matrix that is linear in the variables. This representation allows to use the techniques of robust optimization, to derive a bound based on semidefinite programming. The quality of the bound is investigated using a technique inspired by Nemirovski and Ben-Tal (2002).

Related entries:
- A. d'Aspremont, F. Bach, L. El Ghaoui. Optimal Solutions for Sparse Principal Component Analysis.

Bibtex reference:

@unpublished{Elg:06,
	Author = {L. {El Ghaoui}},
	Month = {February},
	Note = {arXiv:math/060144},
	Title = {On the Quality of a Semidefinite Programming
	Bound for Sparse Principal Component Analysis},
	Year = {2006}}