Recovery of Sparse Probability Measures via Convex Programming

Download: .pdf

Authors: Mert Pilanci, Laurent El Ghaoui, and Venkat Chandrasekaran

Status: In Proc. Advances in Neural Information Processing Systems (NIPS), December 2012.

Abstract: We consider the problem of cardinality penalized optimization of a convex function over the probability simplex with additional convex constraints. The classical 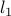regularizer fails to promote sparsity on the probability simplex since 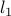norm on the probability simplex is trivially constant. We propose a direct relaxation of the minimum cardinality problem and show that it can be efficiently solved using convex programming. As a first application we consider recovering a sparse probability measure given moment constraints, in which our formulation becomes linear programming, hence can be solved very efficiently. A sufficient condition for exact recovery of the minimum cardinality solution is derived for arbitrary affine constraints. We then develop a penalized version for the noisy setting which can be solved using second order cone programs. The proposed method outperforms known rescaling heuristics based on l1 norm. As a second application we consider convex clustering using a sparse Gaussian mixture and compare our results with the well known soft 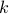-means algorithm.

Bibtex reference:

@conference{PEC:12,
  Author = {Mert Pilanci and Laurent {El Ghaoui} and Venkat Chandrasekaran},
  Title = {Recovery of Sparse Probability Measures via Convex Programming},
  Booktitle= {Proc. Advances in Neural Information Processing Systems ({NIPS})},
  Year = {2012},
  Month = dec
}