A Convex Upper Bound on the Log-Partition Function for Binary Graphical Models

Download: .pdf

Authors: L. El Ghaoui, A. Gueye.

Status: In Proc. NIPS, December 2008.

Abstract: We consider the problem of bounding from above the log-partition function corresponding to second-order Ising models for binary distributions. We introduce a new bound, the cardinality bound, which can be computed via convex optimization. The corresponding error on the log-partition function is bounded above by twice the distance, in model parameter space, to a class of ‘‘standard’’ Ising models, for which variable inter-dependence is described via a simple mean field term. In the context of maximum-likelihood, using the new bound instead of the exact log-partition function, while constraining the distance to the class of standard Ising models, leads not only to a good approximation to the log-partition function, but also to a model that is parsimonious, and easily interpretable. We compare our bound with the log-determinant bound introduced by Wainwright and Jordan (2006), and show that when the 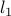-norm of the model parameter vector is small enough, the latter is outperformed by the new bound.

Related entries:
- Technical report UC/EECS-2007-146, December 2007.

Bibtex reference:

@conference{ElN:08,
	Author = {L. {El Ghaoui} and A. Gueye},
	Booktitle = {Proc. NIPS},
	Title = {A convex upper bound on the log-partition function
for binary graphical models},
	Year = {2008}}