CS267: Supplemental Notes for Lecture 17, Mar 12 1996

How Multigrid Damps High Frequencies

Here is a simple explanation of why weighted Jacobi damps the high frequencies in the error of the solution of the discrete Poisson equation. As described in Lecture 17, we want to solve the 1D Poisson equation, T(i)*x(i)=b(i) on a grid with 2^i-1 unknowns, where

                     [  2  -1                 ] 
                     [ -1   2  -1             ]
     T(i) = 4^(-i) * [     -1   2  -1         ]
                     [       ... ... ...      ]
                     [             -1  2  -1  ]
                     [                -1   2  ]

Weighted Jacobi is defined as

   improved x(i)(j) = (1/3)*( x(i)(j-1) + x(i)(j) + x(i)(j+1) + b(i)(j) )

One can confirm that one step of weighted Jacobi can also be written

   improved x(i) = x(i) - (1/3)* 4^i * ( T(i)*x(i) - b(i) )

The exact solution, xtrue(i), satisfies

   xtrue(i) = xtrue(i) - (1/3)* 4^i * ( T(i)*xtrue(i) - b(i) )

Subtracting these equations, and letting error(i) = x(i)-xtrue(i), yields,

   improved error(i) = (I - (1/3)* 4^i * T(i)) * error(i)

In other words, the error vector error(i) is multiplied by the matrix I-(1/3)*4^i*T(i) at each step. Recalling that we can write error(i) as a linear combination of eigenvectors v(j) of T(i)

       error(i) = sum_{j=1} beta(j) * v(j)

let us see what happens to component beta(j) * v(j) of the error after multiplying it by I-(1/3)*4^i*T(i). Since v(j) is an eigenvector of T(i), we have

      T(i) * v(j) = lambda(j) * v(j)  where lambda(j) = 4^(-i)*2*(1-cos(j*pi/(2^i)))

Thus

      (I - (1/3)*4^i*T(i)) * v(j) = (1 - (1/3)*4^i*lambda(j)) * v(j)
                                  = ( (1/3) + (2/3)*cos(j*pi/2^i)) )* v(j)

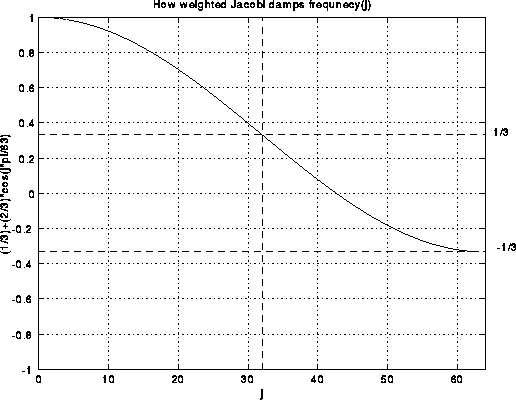
If we plot the coefficient (1/3) + (2/3)*cos(j*pi/2^i)) versus j, we get the following:

Thus, the upper half of the frequencies (demarcated by the dotted lines) are multiplied by a number between -1/3 and 1/3. This means weighted Jacobi decrease the high frequency error by at least a factor of 3 at each step.