
 SPIE '98
SPIE '98

|
CWhatUC A Visual Acuity Simulator |
|---|---|
|
Daniel D. Garcia
(ddgarcia@cs.berkeley.edu)
Brian A. Barsky (barsky@cs.berkeley.edu) Stanley A. Klein (klein@adage.berkeley.edu) The OPTICAL Research Project University of California, Berkeley |
|
|
BACKGROUND The Cornea |
| The cornea is the transparent tissue covering the front of the eye. It performs 3/4 of the refraction, or bending, of light in the eye, and focuses light towards the lens and the retina. Thus, subtle variations in the shape of the cornea can significantly diminish visual performance. | |

|
BACKGROUND Measurement |
| Recently, instruments to measure corneal topography have become commercially available. These corneal topography devices typically shine rings of light onto the cornea and then capture the reflection pattern with a built-in video camera. | |

|
BACKGROUND Reconstruction |
| Instead of allowing the instrument to process the pattern, we at the OPTICAL project extract the data and construct a mathematical spline surface representation from these reflection patterns, as is described in our ACM SIGGRAPH '96 paper, "Reconstructing Curved Surfaces From Specular Reflection Patterns Using Spline Surface Fitting of Normals" | |
|
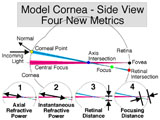
THE FOUR NEW METRICS |
Once we have the shape as a mathematical surface, we perform calculations on its shape. The four calculations are:
|
|

|
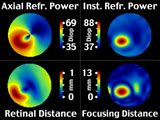
RESULTS Simulated Data |
We use a simple ellipsoid to simulate the cornea here.
The equation for the ellipsoid is (with A=8.7, B=9 and C=10):
|
|
|
RESULTS Real Data |
This data is from a patient with keratoconus, a corneal condition, and
in the lower left there is an oval region of locally high curvature.
|
|

|
CONCLUSION |
We have presented four metrics for simulating visual acuity based on
geometric optics, and shown the results using simulated and real data.
|