 |
(Title Screen)
|
 |
At the University of California at Berkeley, the OPTICAL project is a
multidisciplinary effort in the Computer Science Division and School
of Optometry.
|
 |
"OPTICAL" is an acronym for "OPtics and Topography
Involving the Cornea And Lens". This project is concerned with the
computer-aided measurement, modeling, reconstruction, and
visualization of the shape of the human cornea, called corneal
topography.
|
 |
The cornea is the transparent tissue covering the front of the eye.
|
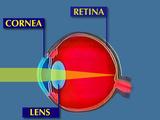 |
It performs 3/4 of the refraction, or bending, of light in the eye,
and focuses light towards the lens and the retina. Thus, subtle
variations in the shape of the cornea can significantly diminish
visual performance.
|
 |
Eye care practitioners need to know the shape of a patient's cornea to
fit contact lenses,
|
 |
to plan and evaluate the results of surgeries that
improve vision by altering the shape of the cornea,
|
 |
and to diagnose
keratoconus, an eye condition where the cornea has an irregular shape
with a local protrusion, called a "cone", which has dramatic effects on
vision.
|
 |
(Summarized reasons why eye clinicians need to know the shape of patients' corneas)
|
 |
Recently, instruments to measure corneal topography have become
commercially available.
|
 |
These devices, called videokeratographs,
|
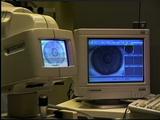 |
typically shine rings of light onto the cornea
|
 |
and then capture the reflection pattern with a built-in video camera.
|
 |
Instead of allowing the instrument to process the pattern, we at the
OPTICAL project extract the data and construct a mathematical spline
surface representation from these reflection patterns.
|
 |
Our task is to construct
|
 |
a model of the cornea
|
 |
from this image and from the geometry of the videokeratograph's source pattern.
For purposes of illustration, we have shrunk the source pattern to a fraction
of its normal size here.
|
 |
We will use a simplified source pattern to illustrate the algorithm more
easily.
|
 |
We begin our construction by guessing
|
 |
a possible surface shape.
|
 |
(We rotate the camera to convey the 3-dimensional nature of the scene and to end up looking toward the right side of the scene)
|
 |
Then we measure
|
 |
the difference between
|
 |
the surface that we have guessed
|
 |
and the real cornea.
|
 |
First we identify features in the image
|
 |
(In the video, the red dot on the left blinks to indicate it's one of the features we were talking about)
|
 |
and their corresponding points in the source pattern. (The corresponding red point blinks too)
|
 |
(The corresponding green points blink)
|
 |
(The corresponding blue points blink)
|
 |
(Now we rotate the camera back so that we end up looking at the scene straight on, as in the beginning)
|
 |
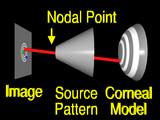
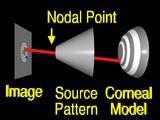
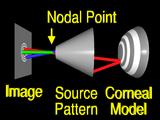
If we assume that the lens system can be modeled by
|
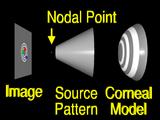 |
a pinhole or nodal point, we can simulate the process that formed the image by using backward ray tracing.
|
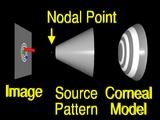 |
A ray from an image feature
|
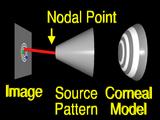 |
is traced through the nodal point
|
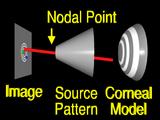 |
to the surface.
|
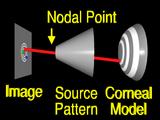 |
If the surface that we guessed has the correct local shape,
|
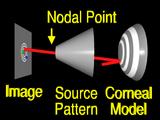 |
the ray will intersect the source pattern
|
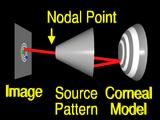 |
at the corresponding feature. (Yeah!)
|
 |
More commonly,
|
 |
the surface is incorrect, (the surface changes shape to represent an incorrect guess)
|
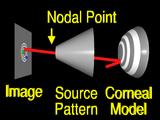 |
so the ray
|
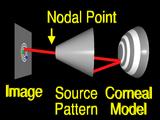 |
misses the feature. (Startled "Huh!") The aim is to change the surface so that the ray
intersects the correct location.
However, we must change the shape of the surface globally, otherwise
|
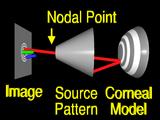 |
rays from other features
|
 |
will still
|
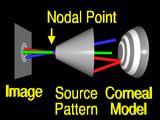 |
miss
|
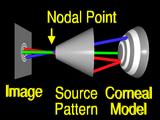 |
their
|
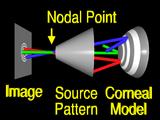 |
corresponding
|
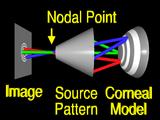 |
features. (Homer says "Explain How!")
|
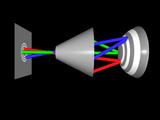 |
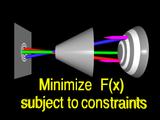
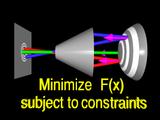
The appropriate global change is computed using constrained optimization.
|
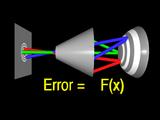 |
From the traced rays we formulate an error function that measures the
difference between the guessed surface and the true cornea.
|
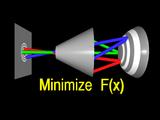 |
The surface that minimizes this error function has a simular shape to the
true cornea.
|
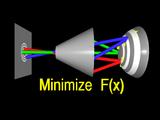 |
In order to make the problem more easily solved, we constrain the surface
to interpolate one or more points.
|
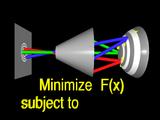 |
These constraints and the error function define
|
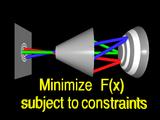 |
a standard constrained
minimization problem.
|
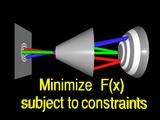 |
We solve this problem iteratively, by taking an initial guess,
|
 |
and stepping toward the solution. (The rays are animated as they move toward the solution)
|
 |
We have carefully formulated the error function and chosen a surface
representation so that each step can be performed efficiently.
|
 |
Each iteration requires
|
 |
tracing
|
 |
rays,
|
 |
computing
|
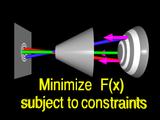 |
a set of normals,
|
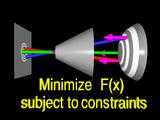 |
and fitting a new surface (the surface changes shape to indicate the fitting is taking place)
|
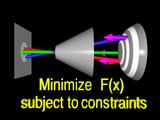 |
to the normals.
|
 |
In our case, we can fit the normals by solving a linear system. (Rays trace back to source pattern to indicate the new surface is correct)
|
 |
In addition to developing this novel modeling algorithm, we are exploring
new scientific visualization techniques to display the resulting
information in an intuitive and accurate manner. This video compares
our new visualization methods with existing techniques.
|
 |
Using our modeling and visualization software, we will first show real
keratoconic data
|
 |
and then a simulated keratoconic model.
|
 |
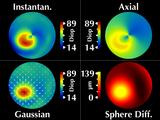
The most popular display of corneal topography is called the "corneal
map". This is similar to a topographic map
|
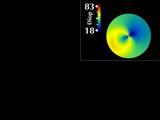 |
where equal values of some parameter are displayed in the same color.
|
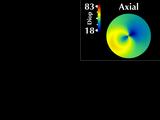 |
The usual parameter that is displayed is called axial curvature
|
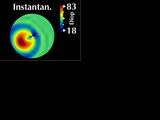 |
and instantaneous curvature.
However, as we will show, this can produce misleading results.
We are proposing alternative parameters, "Gaussian
power with cylinder", that overcome these problems.
|
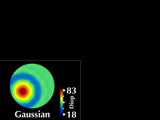 |
Gaussian power is related to the geometric mean of the maximum and minimum
curvatures at each data point and cylinder is related to their difference.
|
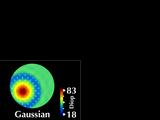 |
We display both parameters simultaneously by superimposing a cylinder
vector field on the Gaussian power map.
|
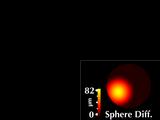 |
To compare with a more direct representation, we include a height map
computed as the radial difference in microns between the surface and
the best-fit sphere.
|
 |
We compute the
values of these parameters using our reconstructed spline surface
model.
|
 |
Let's look at the corneal data from the patient we saw being
measured earlier.
|
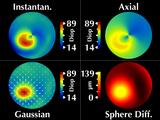 |
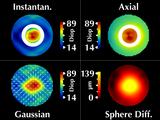
His cornea has a cone in the lower right (our left). These four
windows all display the same data, which we call "regular fixation"
since the patient is looking directly into the videokeratograph.
|
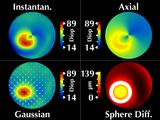 |
Considering the cone region, we note several interesting features.
First, the cone is rotationally symmetric, as revealed by our sphere
difference map.
|
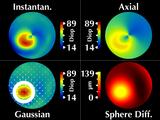 |
Our Gaussian map reflects this symmetry,
|
 |
but the instantaneous and axial curvature maps do not.
|
 |
More importantly, they have significantly different values for the
maximum curvature at the cone.
|
 |
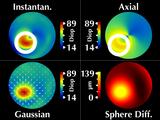
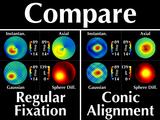
Now let's examine how the corneal maps change when the patient
shifts his gaze up toward his left so that the cone aligns with
the center of the videokeratograph; we call this "conic alignment".
|
 |
The sphere difference map remains rotationally symmetric, as it should,
and is aligned with the center of the videokeratograph axis.
|
 |
We can make several observations:
First, our Gaussian map remains relatively rotationally symmetric.
|
 |
The Axial and Instantaneous curvature maps are rotationally
symmetric for conic alignment, but were not for regular fixation.
|
 |
The maximum value at the cone for instantaneous curvature is
the same as for axial curvature.
|
 |
Now let's examine the two gaze directions together.
|
 |
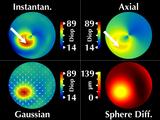
As we compare the two representations, we note an important
difference:
|
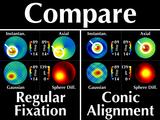 |
For different gaze directions, the shape and values of the
cone region as depicted in the axial and instantaneous curvature
maps differ ("Doh!")
|
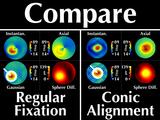 |
but remain invariant with our Gaussian power map. ("Woo hoo!")
|
 |
In other words, by simply changing the direction of the patient's
gaze, axial and instantaneous curvatures yield two conflicting
descriptions of the cone (crowd makes "startle" sound)
whereas our proposed visualization does not have this problem. (crowd says "yay!")
|
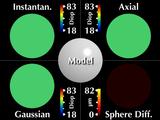 |
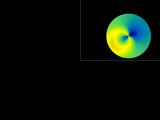
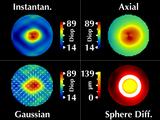
Now let's consider a simulated cornea. These five windows all display
the same keratoconic model. The center animation indicates how we
scale and move the cone around, while the other images show corneal
maps displaying different parameters.
|
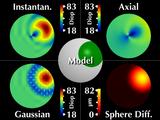 |
The model of our simulated cone is rotationally symmetric, and
maintains a constant shape when moving across and around the
cornea.
|
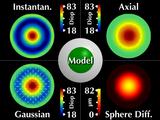 |
Our two new visualizations faithfully represent the symmetry
and shape invariance.
|
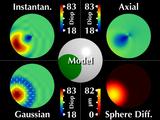 |
However, axial and instantaneous curvature fail on both accounts,
erroneously showing the cone region as significantly changing shape as
it moves around and across the cornea, which is what we saw earlier.
|
 |
This video has shown how the OPTICAL project is developing new
computer aided cornea modeling and visualization techniques to enable
eye care clinicians to help people overcome some of their difficult
vision problems.
|
 |
Roll credits.
|
 |
 |
 |
 |
 |
 |
 Our SIGGRAPH '96 Electronic Theatre Video Redone
Our SIGGRAPH '96 Electronic Theatre Video Redone
