
|
Figure 1
|
|
A meridional plane, depicted as an orange plane. This plane contains the corneal point of interest (shown as a green dot) and the videokeratograph axis (depicted as a red vector).
|
|
|
|
|
Figure 2
|
|
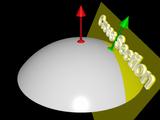
The yellow cross-sectional plane contains the normal vector at the point of interest (shown as a green dot). This diagram differs from the one published in that this one has a green vector through the point of interest to indicate the surface normal at that point.
|
|
|
|

|
Figure 3
|
|
Ths planes corresponding to the minimum and maximum curvature directions are shown in blue and red, respectively. This diagram differs from the one published in that this one has a green vector through the point of interest to indicate the surface normal at that point.
|
|
|
|

|
Figure 4
|
|
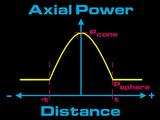
This graph illustrates the base corneal model without keratoconus. The model
is a
simple sphere with constant axial power across its surface. This
is represented here as a yellow straight line when plotting axial power vs. diatance. The power is denoted Psphere, and is labeled in red.
|
|
|
|
|
Figure 5
|
|
To model keratoconus, a section of the sphere is removed and replaced with a surface of revolution formed from a hyperbola. The axial power associated with the hyperbola between -t and t is shown as the yellow curve. The maximum power of the cone is denoted Pcone.
|
|
|
|
_160.jpg)
|
Figure 6(i)
|
|
This shows a mock-up, depicting in each figure component 6(i) thorugh 6(v), the center of the simulated cone (middle), instantaneous power (upper left), axial power (upper right), Gaussian power with a cylinder overlay (lower left), and the height map, or radial difference from the reference sphere (lower right). The center of the cone is at phi = 12° and theta = 215°. Here Pcone = Psphere = 45 D; thus, there is no keratoconus and all power maps are constant.
|
|
|
|
_160.jpg)
|
Figure 6(ii)
|
|
Same as Fig. 6(i), except Pcone is set to 57 D of axial power, slightly larger than Psphere. The cone is shown in green in the model.
|
|
|
|
_160.jpg)
|
Figure 6(iii)
|
|
The parameter Pcone has now reached its maximum value of 82 D.
|
|
|
|
_160.jpg)
|
Figure 6(iv)
|
|
The parameter Pcone is fixed at 82 D and the cone is rotated toward the center of the cornea. Its center is now at phi = 6°.
|
|
|
|
_160.jpg)
|
Figure 6(v)
|
|
The center of the cone is now at phi = 0° (directly at the north pole).
|
|
|
|
|
Figure 7
|
|
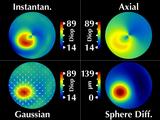
The four views of regular fixation (patient looking directly into the center
of the videokeratograph): instantaneous power (upper left), axial power (upper
right), Gaussian power with a cylinder overlay (lower left), and the radial
difference from a reference sphere (lower right).
|
|
|
|

|
Figure 8
|
|
The four views of conic alignment (patient shifting his gaze direction up
toward his left so that the cone alights with the center
of the videokeratograph): instantaneous power (upper left), axial power (upper
right), Gaussian power with a cylinder overlay (lower left), and the radial
difference from a reference sphere (lower right).
|

 Optometry and Vision Science article
Optometry and Vision Science article




_160.jpg)
_160.jpg)
_160.jpg)
_160.jpg)
_160.jpg)

