Brain Candy Archive
Overview
This is a page of fun puzzles (brain candy) that I've been sent by
friends or which I've read in books. I try to give credit to the
author when possible. I also have a
list of puzzles that will
eventually grace these pages. Additionally, my friend Adam
Costello has some very very excellent puzzles on his puzzles
page.
2001-06 : Heads Up Pennies
Tom & Ray Magliozzi of Car Talk
RAY: You're sitting at a table with a bunch of pennies on it. Some are
facing heads up and some are facing tails up. You're wearing a
blindfold, and you're wearing mittens so that you can't actually feel
the coins and tell which side is facing up. If we could trust you,
we'd let you do it without gloves.
TOM: Well, you know me. I always sit around with mittens and a mask on
anyway.
RAY: I will tell you that a certain number of the pennies are facing
heads up. Let's say 10 are facing heads up.
TOM: You're telling me there are a bunch of pennies in front of me and
10 of them are heads up?
RAY: Right. With your mittens on, you can move the pennies around, you
can pick them up, you can put them down again, you can shake them, you
can do whatever you want. Here's the question: Is it possible to
separate those pennies into two groups, so that each group has the
same number of pennies facing heads up? How do you do it?
2001-06 Solution
2000-01 : Handshakes at a Party
...seen-in-Scientific-American-some-years-ago...
Five married couples attended a party. One of the ten people was a
mathematician. During the party, many people shook hands, but nobody
shook hands with his/her spouse, and nobody shook hands with
him/herself.
The mathematician asked each of the other people, "With how many people
did you shake hands?" Each person gave a different answer.
With how many people did the mathematician's spouse shake hands?
2000-01 Solution
1999-06 : Sum and Product Man
by Syd Reader (sydryck@leland.stanford.edu)
An oracle chooses two whole numbers from the range [2,100]. (That
means the numbers can include 2 and 100, and the two numbers can be
the same) There are two perfect logicians, Sum and Product. The oracle
gives Sum the sum of the two numbers and Product the product of the
two numbers. They have a small conversation:
- Product: I don't know what the numbers are.
- Sum: I knew you didn't know what the numbers were.
- Product: I know what the numbers are.
- Sum: I know what the numbers are.
What are the original two numbers?
1999-05 : Balls on a Ring
by Osana Tishkova (Osana.Tishkova@eng.sun.com)
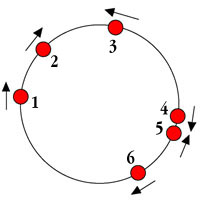 Welcome to perfect physics world. Imagine a circular frictionless
bracelet with numbered balls randomly placed on it as in the example to the
right. Each ball is traveling either clockwise or counter-clockwise at
the same constant angular velocity. All collisions are elastic, i.e.,
no energy is lost and immediately afterwards the balls bounce back
from whence they came. The balls do not compress during collision,
and have non-zero diameter.
Welcome to perfect physics world. Imagine a circular frictionless
bracelet with numbered balls randomly placed on it as in the example to the
right. Each ball is traveling either clockwise or counter-clockwise at
the same constant angular velocity. All collisions are elastic, i.e.,
no energy is lost and immediately afterwards the balls bounce back
from whence they came. The balls do not compress during collision,
and have non-zero diameter.
The initial condition is simply the position and direction of travel
of the balls. Assume it would take one unit of time for one ball to
travel a full revolution without collisions.
Questions
- Are you guaranteeed that the initial condition will
eventually repeat? I.e., ball number 1 is at the same position going the
same direction, similarly for all the other balls.
- Prove your answer.
- If you can guarantee that the initial position will repeat, can you predict when it will? I.e., describe, as a closed function of the input position, how long it will take to repeat.
1998-09 : Pairing up students
by John Corzine (jcorzine@spectacle.berkeley.edu)
Assume you have n students. You would like to have lab sections in
which every student chooses a partner to work together for that
particular lab section. Over the course of the semester, you'd like
to have every student work with every other student exactly once. As
there are n students, this can be done in n-1 days optimally. How is
it done? (e.g. show how to pair 20 students up)
1998-09 Solution
1998-04 : Guess-the-Animal
by Walter McKay (printed in Ask Marilyn, 97-04-05)
- Pick a number from 1 through 9.
- Subtract 5 from the number (negative results are ok)
- Multiply the result by 3.
- Square the result.
- Add the digits of the result until there's only one digit. (Example: 64. 6+4=10. 1+0=1.)
- If the result is less than 5, add 5; if not, subtract 4.
- Multiply the result by 2.
- Subtract 6 from the result.
- Locate the corresponding letter in the alphabet. (Examples: 1=A, 2=B.)
- Pick a country that begins with that letter.
- Note the second letter in that country's name. Think of a mammal that begins with that letter.
- Now think of the color of that mammal. What do you have? (And why did I know it was a grey elephant from Denmark?)
1998-04 Solution
1997-08 : Men & Women
by Warren Buckland (printed in Ask Marilyn, 97-08-10)
An explorer is in a strange land where the men always tell the truth and the women always lie. He meets three natives but cannot tell their sex by their appearance or voice, so he asks them.
The first one replies, but the explorer doesn't hear the answer. The second one makes the following three statements:
- The first person said, "I am a man"
- The first person is a woman
- I am a man
The third one makes these two statements:
- The second person is a woman
- I am a man
Which are men, and which are women?
1997-08 Solution
1997-06 : Miracle-Fold Maps
by John D., LA, CA (printed in Ask Marilyn, 97-05-04)
Divide a sheet of paper into eight parts. Number them on one side as in the
diagram. The problem is to fold the paper (along the lines) to form a
packet (like a folded map) with No. 1 face up on top, followed by the other
numbers in order.
1997-06 Solution
1997-05 : Stuck on a Train Bridge
by Chuck Minnich, Albany GA (printed in Ask Marilyn, 97-04-27)
A man is walking across a railroad bridge spanning a river. When he is
7/10 of the way across, he hears a train coming. Fortunately for him, no
matter which way he runs at top speed, he can just make it to the end and
jump clear as the train misses him. The train is traveling 60mph. How fast
can the man run?
1997-05 Solution
1997-03 : The Liar and the Truthteller
by Not-Sure-I-Heard-It-Long-Ago (retold to me by James Hopkin) james@nwcs.net
You meet two natives from different villages at a crossroads. One
always lies and one always tells the truth, but you doesn't know which
is which. You need to find out whether the left or right path leads to
safety, but can only ask one of them a single question. What should
you ask (and what should you do depending on what they answer)?
1997-03 Solution
1997-02 : Frogs and Lightbulbs
by Not-Sure-I-Heard-It-Long-Ago
You have 100 lightbulbs, numbered 1-100, and 100 frogs, also numbered 1-100.
Whenever a frog jumps on a lightbulb, it toggles between on and off.
All lightbulbs are initially off.
- frog #1 jumps on every lightbulb (ie turning them all on).
- frog #2 jumps on every 2nd lightbulb, toggling some of them back off.
- ...
- frog #k jumps on every kth lightbulb.
After 100 frogs, which ones are on?
1997-02 Solution
1997-01 : Sweet Liar Problem
by Barry R. Clarke (from "Test Your Puzzle Power")
Only one of John, Alice or Frank has sweets. John says that Alice does not
have sweets; Alice says that neither John nor herself has sweets; Frank
says that either John or Alice has sweets. If only one of them is telling the
truth, who has the sweets?
1997-01 Solution
1996-12 : The missing digit
by A-Student-Of-Alex-Berg (alex@ads.com)
Given:
ABCD
- BDCA
------
119?
Where A,B,C,D are digits, what is
the missing digit, the ?
1996-12 Solution
1996-11 : Infinite Baseball Games
by Not-Sure-I-Heard-It-Long-Ago
Name all the ways to extend a baseball game indefinitely. The methods
have to be ones in which the umpires have no say. So a solution in which
the pitcher just held the ball and didn't pitch wouldn't work, because
the umpires could order the pitcher to pitch the ball and they would have
a say.
1996-11 Solution
1996-10 : Recombinant Numbers - Infinite or Finite Set?
by Someone-who-sent-this-into-MITs-Technology-Review
Recombinant numbers are numbers whose digits can be recombined by simple
mathematical expressions to form the number themselves. e.g. 25 = 52,
125 = 5(1+2), 625=5(6-2), 3215=5(3+2)*1,
15625=5(1+5+6)/2, 78125=5(7*2-8-1), 390625=5(7*((3*9*0)+6+2)
Question: Is the set of recombinant numbers finite or infinite?
1996-10 Solution
1996-09 : Triomino  tiling of 2n-sided square
tiling of 2n-sided square
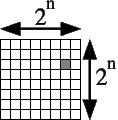
by David Blackston (davidb@cs.berkeley.edu)
Imagine a chessboard that is 2n by 2n on a side.
Remove one square anywhere on the chessboard. Prove by induction that you
can tile the remaining chessboard with triominoes. (A triomino is an L-shaped
piece containing 3 squares, which could be formed by gluing the chess squares
a1, a2 and b1 together, which looks like:  )
)
1996-09 Solution
1996-08 : Repeated Fraction Puzzle
by A-guy-I-men-on-the-Boston-Houston-960812-evening-flight
Find a simple counting number (1,2,3,...) denominator, n, which has
a repeating decimal equivalent 1/n (e.g. 3 has 1/3 = .333...) but whose
multiples (2/n, 3/n, 4/n, etc) are themselves the EXACT same repeating
decimal, just starting at a different place in the pattern.
1996-08 Solution
1996-07 : Two Children
by Ross Levinsky (rblevins@athena.mit.edu)
Man #1 says he has two children. One of them is a boy. What's the chance
his other one is a girl? (supplementary question: Man #2 says he has two
children. His first one is a boy. What's the chance the other one
is a girl?)
1996-07 Solution
1996-02 : Fold a buck and make a triangle
by Barry R. Clarke (from "Test Your Puzzle Power")
Fold a dollar bill into a triangle using the least number of folds.
1996-02 Solution
1995-12 : Three quickies
by Scott Winokur and The National Assessment of Educational Progress
Three you're-only-allowed-to-do-these-in-your-head quickies:
- Approx. what is 15/16 plus 7/8? (options: 1, 2, 19, 20)
- What is the sum of all of the integers from 1 through 100 inclusive?
- What is the one's digit of the number 2312?
1995-12 Solution
1995-11 : The unmarked clock
by Yeh-Kai Tung (yktung@physics.Berkeley.EDU)
You are given a clock with the numbers removed and all but one of the
number markers also removed, leaving the minute and hour hands and one
of the hour markers (but you don't know which one). The clock is circular,
so you can't tell the original orientation of it. With just a protractor
(Protractor?! But I just met her!) and your logic, how can you instantaneously
determine both the exact time and the original positions and numbering
of the other 12 dots?
1995-11 Solution
WWW Maven: Dan
Garcia (ddgarcia@cs.berkeley.edu)
 Send me feedback
Send me feedback




 Welcome to perfect physics world. Imagine a circular frictionless
bracelet with numbered balls randomly placed on it as in the example to the
right. Each ball is traveling either clockwise or counter-clockwise at
the same constant angular velocity. All collisions are elastic, i.e.,
no energy is lost and immediately afterwards the balls bounce back
from whence they came. The balls do not compress during collision,
and have non-zero diameter.
Welcome to perfect physics world. Imagine a circular frictionless
bracelet with numbered balls randomly placed on it as in the example to the
right. Each ball is traveling either clockwise or counter-clockwise at
the same constant angular velocity. All collisions are elastic, i.e.,
no energy is lost and immediately afterwards the balls bounce back
from whence they came. The balls do not compress during collision,
and have non-zero diameter.
