


|
|
| I know an old lady who swallowed a fly. | She swallowed the cat to catch the bird. |
| I don't know why she swallowed the fly. | She swallowed the bird to catch the spider |
| Perhaps she'll die. | that wriggled and jiggled and tickled inside her. |
| She swallowed the spider to catch the fly. | |
| I know an old lady who swallowed a spider | I don't know why she swallowed the fly. |
| that wriggled and jiggled and tickled inside her. | Perhaps she'll die. |
| She swallowed the spider to catch the fly. | |
| I don't know why she swallowed the fly. | I know an old lady who swallowed a dog. |
| Perhaps she'll die. | What a hog, to swallow a dog! |
| She swallowed the dog to catch the cat. | |
| I know an old lady who swallowed a bird. | She swallowed the cat to catch the bird. |
| How absurd, to swallow a bird! | She swallowed the bird to catch the spider |
| She swallowed the bird to catch the spider | that wriggled and jiggled and tickled inside her. |
| that wriggled and jiggled and tickled inside her. | She swallowed the spider to catch the fly. |
| She swallowed the spider to catch the fly. | I don't know why she swallowed the fly. |
| I don't know why she swallowed the fly. | Perhaps she'll die. |
| Perhaps she'll die. | |
| I know an old lady who swallowed a horse. | |
| I know an old lady who swallowed a cat. | She's dead of course! |
| Imagine that, to swallow a cat. | |
| 100 bottles of beer on the wall, | 98 bottles of beer on the wall, |
| 100 bottles of beer. | 98 bottles of beer. |
| If one of those bottles should happen to fall, | If one of those bottles should happen to fall, |
| 99 bottles of beer on the wall. | 97 bottles of beer on the wall. |
| 99 bottles of beer on the wall, | 97 bottles of beer on the wall, |
| 99 bottles of beer. | 97 bottles of beer. |
| If one of those bottles should happen to fall, | If one of those bottles should happen to fall, |
| 98 bottles of beer on the wall. | 96 bottles of beer on the wall… |
In the next few chapters we're going to talk about recursion: solving a big problem by reducing it to a similar, smaller subproblem. Actually that's a little backward from the old lady in the song, who turned her little problem into a similar but bigger problem! As the song warns us, this can be fatal.
Here's the first problem we'll solve. We want a function that works like this:
> (downup 'ringo) (RINGO RING RIN RI R RI RIN RING RINGO) > (downup 'marsupial) (MARSUPIAL MARSUPIA MARSUPI MARSUP MARSU MARS MAR MA M MA MAR MARS MARSU MARSUP MARSUPI MARSUPIA MARSUPIAL)
None of the tools that we've used so far will handle this problem. It's not
a "compute this function for each letter of the word" problem, for which
we could use every.[1] Rather, we have to think
about the entire word in a rather complicated way.
We're going to solve this problem using recursion. It turns out that the idea of recursion is both very powerful—we can solve a lot of problems using it—and rather tricky to understand. That's why we're going to explain recursion several different ways in the coming chapters. Even after you understand one of them, you'll probably find that thinking about recursion from another point of view enriches your ability to use this idea. The explanation in this chapter is based on the combining method.
Since we don't yet know how to solve the downup problem in general,
let's start with a particular case that we can solve. We'll write a
version of downup that works only for one-letter words:
(define (downup1 wd) (se wd)) > (downup1 'a) (A)
So far so good! This isn't a very versatile program, but it does have the advantage of being easy to write.
Now let's see if we can do two-letter words:
(define (downup2 wd) (se wd (first wd) wd)) > (downup2 'be) (BE B BE)
Moving right along…
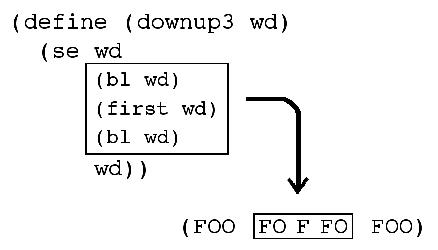
(define (downup3 wd)
(se wd
(bl wd)
(first wd)
(bl wd)
wd))
> (downup3 'foo)
(FOO FO F FO FOO)
We could continue along these lines, writing procedures downup4 and so
on. If we knew that the longest word in English had 83 letters, we could
write all of the single-length downups up to downup83, and then
write one overall downup procedure that would consist of an enormous
cond with 83 clauses, one for each length.
But that's a terrible idea. We'd get really bored, and start making a lot
of mistakes, if we tried to work up to downup83 this way.
The next trick is to notice that the middle part of what (downup3 'foo) does is just like (downup2 'fo):
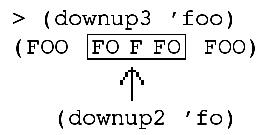
So we can find the parts of downup3 that are responsible for
those three words:
and replace them with an invocation of downup2:
(define (downup3 wd) (se wd (downup2 (bl wd)) wd))
How about downup4? Once we've had this great idea about using downup2 to help with downup3, it's not hard to continue the pattern:
(define (downup4 wd) (se wd (downup3 (bl wd)) wd)) > (downup4 'paul) (PAUL PAU PA P PA PAU PAUL)
The reason we can fit the body of downup4 on one line is that most of
its work is done for it by downup3. If we continued writing each new
downup procedure independently, as we did in our first attempt at downup3, our procedures would be getting longer and longer. But this new
way avoids that.
(define (downup59 wd) (se wd (downup58 (bl wd)) wd))
Also, although it may be harder to notice, we can even rewrite downup2
along the same lines:
(define (downup2 wd) (se wd (downup1 (bl wd)) wd))
Although downup59 was easy to write, the problem is that it won't work
unless we also define downup58, which in turn depends on downup57, and so on. This is a lot of repetitive, duplicated, and
redundant typing. Since these procedures are all basically the same, what
we'd like to do is combine them into a single procedure:
(define (downup wd) ;; first version (se wd (downup (bl wd)) wd))
Isn't this a great idea? We've written one short procedure that serves as a kind of abbreviation for 59 other ones.
Unfortunately, it doesn't work.
> (downup 'toe) ERROR: Invalid argument to BUTLAST: ""
What's gone wrong here? Not quite every numbered downup looks like
(define (downupn wd) (se wd (downupn-1 (bl wd)) wd))
The only numbered downup that doesn't follow the pattern is downup1:
(define (downup1 wd) (se wd))
So if we collapse all the numbered downups into a single procedure, we
have to treat one-letter words as a special case:
(define (downup wd)
(if (= (count wd) 1)
(se wd)
(se wd (downup (bl wd)) wd)))
> (downup 'toe)
(TOE TO T TO TOE)
> (downup 'banana)
(BANANA BANAN BANA BAN BA B BA BAN BANA BANAN BANANA)
This version of downup will work for any length word, from a to
pneumonoultramicroscopicsilicovolcanoconinosis[2] or beyond.
Downup illustrates the structure of every recursive procedure. There is
a choice among expressions to evaluate: At least one is a recursive
case, in which the procedure (e.g., downup) itself is invoked with a
smaller argument; at least one is a base case, that is, one that can
be
solved without calling the procedure recursively. For downup, the base
case is a single-letter argument.
How can this possibly work? We're defining downup in terms of downup. In English class, if the teacher asks you to define "around,"
you'd better not say, "You know, around!" But we appear to be
doing just that. We're telling Scheme: "In order to find downup of a
word, find downup of another word."
The secret is that it's not just any old other word. The new word is
smaller than the word we were originally asked to downup. So
we're saying, "In order to find downup of a word, find downup
of a shorter word." We are posing a whole slew of subproblems
asking for the downup of words smaller than the one we started with.
So if someone asks us the downup of happy, along the way we have
to compute the downups of happ, hap, ha, and h.
A recursive procedure doesn't work unless every possible argument can
eventually be reduced to some base case. When we are asked for downup
of h, the procedure just knows what to do without calling itself
recursively.
We've just said that there has to be a base case. It's also important that
each recursive call has to get us somehow closer to the base case. For
downup, "closer" means that in the recursive call we use a shorter
word. If we were computing a numeric function, the base case might be an
argument of zero, and the recursive calls would use smaller numbers.
Let's take another example; we'll write the Pig Latin procedure that we showed off in Chapter 1. We're trying to take a word, move all the initial consonants to the end, and add "ay."
The simplest case is that there are no initial consonants to move:
(define (pigl0 wd) (word wd 'ay)) > (pigl0 'alabaster) ALABASTERAY
(This will turn out to be the base case of our eventual recursive procedure.)
The next-simplest case is a word that starts with one consonant. The obvious way to write this is
(define (pigl1 wd) ;; obvious version (word (bf wd) (first wd) 'ay)) > (pigl1 'salami) ALAMISAY
but, as in the downup example, we'd like to find a way to use
pigl0 in implementing pigl1. This case isn't exactly like downup, because there isn't a piece of the return value that we can draw a
box around to indicate that pigl0 returns that piece. Instead, pigl0 puts the letters ay at the end of some word, and so does pigl1. The difference is that pigl1 puts ay at the end of
a rearrangement of its argument word. To make this point clearer,
we'll rewrite pigl1 in a way that separates the rearrangement from the
ay addition:
(define (pigl1 wd) (word (word (bf wd) (first wd)) 'ay)) > (pigl1 'pastrami) ASTRAMIPAY
Now we actually replace the pigl0-like part with an
invocation. We want to replace (word with
something 'ay)(pigl0 . If we use something)pigl0 to attach the
ay at the end, our new version of pigl1 looks like this:
(define (pigl1 wd) (pigl0 (word (bf wd) (first wd))))
How about a word starting with two consonants? By now we know that we're
going to try to use pigl1 as a helper procedure, so let's skip writing
pigl2 the long way. We can just move the first consonant to the end
of the word, and handle the result, a word with only one consonant in front,
with pigl1:
(define (pigl2 wd) (pigl1 (word (bf wd) (first wd)))) > (pigl2 'trample) AMPLETRAY
For a three-initial-consonant word we move one letter to the end and call
pigl2:
(define (pigl3 wd) (pigl2 (word (bf wd) (first wd)))) > (pigl3 'chrome) OMECHRAY
So how about a version that will work for any word?[3] The recursive case will involve taking the pigl of (word (bf wd) (first wd)), to match the pattern we found in
pigl1, pigl2, and pigl3. The base case will be a word
that begins with a vowel, for which we'll just add ay on the end, as
pigl0 does:
(define (pigl wd)
(if (member? (first wd) 'aeiou)
(word wd 'ay)
(pigl (word (bf wd) (first wd)))))
It's an unusual sense in which pigl's recursive call poses a
"smaller" subproblem. If we're asked for the pigl of scheme,
we construct a new word, chemes, and ask for pigl of that. This
doesn't seem like much progress. We were asked to translate scheme, a
six-letter word, into Pig Latin, and in order to do this we need to
translate chemes, another six-letter word, into Pig Latin.
But actually this is progress, because for Pig Latin the base case
isn't a one-letter word, but rather a word that starts with a vowel.
Scheme has three consonants before the first vowel; chemes has
only two consonants before the first vowel.
Chemes doesn't begin with a vowel either, so we construct the word
hemesc and try to pigl that. In order to find (pigl 'hemesc) we need to know (pigl 'emesch). Since emesch
does begin with a vowel, pigl returns emeschay. Once we
know (pigl 'emesch), we've thereby found the answer to our original
question.
You've now seen two examples of recursive procedures that we developed using the combining method. We started by writing special-case procedures to handle small problems of a particular size, then simplified the larger versions by using smaller versions as helper procedures. Finally we combined all the nearly identical individual versions into a single recursive procedure, taking care to handle the base case separately.
Here are a couple of problems that can be solved with recursive procedures. Try them yourself before reading further. Then we'll show you our solutions.
> (explode 'dynamite) (D Y N A M I T E) > (letter-pairs 'george) (GE EO OR RG GE)
What's the smallest word we can explode? There's no reason we
can't explode an empty word:
(define (explode0 wd) '())
That wasn't very interesting, though. It doesn't suggest a pattern that will apply to larger words. Let's try a few larger cases:
(define (explode1 wd) (se wd)) (define (explode2 wd) (se (first wd) (last wd))) (define (explode3 wd) (se (first wd) (first (bf wd)) (last wd)))
With explode3 the procedure is starting to get complicated enough that
we want to find a way to use explode2 to help. What explode3
does is to pull three separate letters out of its argument word, and collect
the three letters in a sentence. Here's a sample:
> (explode3 'tnt) (T N T)
Explode2 pulls two letters out of a word and
collects them in a sentence. So we could let explode2 deal with two
of the letters of our three-letter argument, and handle the remaining letter
separately:
(define (explode3 wd) (se (first wd) (explode2 (bf wd))))
We can use similar reasoning to define explode4 in terms of
explode3:
(define (explode4 wd) (se (first wd) (explode3 (bf wd))))
Now that we see the pattern, what's the base case? Our first three
numbered explodes are all different in shape from explode3,
but now that we know what the pattern should be we'll find that we
can write explode2 in terms of explode1, and even explode1
in terms of explode0:
(define (explode2 wd) (se (first wd) (explode1 (bf wd)))) (define (explode1 wd) (se (first wd) (explode0 (bf wd))))
We would never have thought to write explode1 in that
roundabout way, especially since explode0 pays no attention to
its argument, so computing the butfirst doesn't contribute
anything to the result, but by following the pattern we can let the
recursive case handle one-letter and two-letter words, so that only
zero-letter words have to be special:
(define (explode wd)
(if (empty? wd)
'()
(se (first wd) (explode (bf wd)))))
Now for letter-pairs. What's the smallest word we can use as its
argument? Empty and one-letter words have no letter pairs in them:
(define (letter-pairs0 wd) '()) (define (letter-pairs1 wd) '())
This pattern is not very helpful.
(define (letter-pairs2 wd)
(se wd))
(define (letter-pairs3 wd)
(se (bl wd) (bf wd)))
(define (letter-pairs4 wd)
(se (bl (bl wd))
(bl (bf wd))
(bf (bf wd))))
Again, we want to simplify letter-pairs4 by using letter-pairs3
to help. The problem is similar to explode: The value returned by
letter-pairs4 is a three-word sentence, and we can use letter-pairs3 to generate two of those words.
> (letter-pairs4 'nems)
(NE EM MS)
This gives rise to the following procedure:
(define (letter-pairs4 wd)
(se (bl (bl wd))
(letter-pairs3 (bf wd))))
Does this pattern work for defining letter-pairs5 in terms of letter-pairs4?
(define (letter-pairs5 wd) ;; wrong
(se (bl (bl wd))
(letter-pairs4 (bf wd))))
> (letter-pairs5 'bagel)
(BAG AG GE EL)
The problem is that (bl (bl wd)) means "the first two letters of wd" only when wd has four letters. In order to be able to
generalize the pattern, we need a way to ask for the first two letters of a
word that works no matter how long the word is. You wrote a procedure to
solve this problem in Exercise :
(define (first-two wd) (word (first wd) (first (bf wd))))
Now we can use this for letter-pairs4 and letter-pairs5:
(define (letter-pairs4 wd) (se (first-two wd) (letter-pairs3 (bf wd)))) (define (letter-pairs5 wd) (se (first-two wd) (letter-pairs4 (bf wd))))
This pattern does generalize.
(define (letter-pairs wd)
(if (<= (count wd) 1)
'()
(se (first-two wd)
(letter-pairs (bf wd)))))
Note that we treat two-letter and three-letter words as recursive
cases and not as base cases. Just as in the example of explode, we
noticed that we could rewrite letter-pairs2 and letter-pairs3 to
follow the same pattern as the larger cases:
(define (letter-pairs2 wd)
(se (first-two wd)
(letter-pairs1 (bf wd))))
(define (letter-pairs3 wd)
(se (first-two wd)
(letter-pairs2 (bf wd))))
Every recursive procedure must include two parts: one or more recursive
cases, in which the recursion reduces the size of the problem, and one or
more base cases, in which the result is computable without recursion. For
example, our first attempt at downup fell into this pitfall because we
had no base case.
Don't be too eager to write the recursive procedure. As we showed
in the letter-pairs example, what looks like a generalizable
pattern may not be.
11.1 Write downup4 using only the word and sentence primitive procedures.
11.2 [8.12][4]
When you teach a class, people will get distracted if you say "um" too many
times. Write a count-ums that counts the number of times "um"
appears in a sentence:
> (count-ums '(today um we are going to um talk about the combining um method)) 3
Here are some special-case count-ums
procedures for sentences of particular lengths:
(define (count-ums0 sent)
0)
(define (count-ums1 sent)
(if (equal? 'um (first sent))
1
0))
(define (count-ums2 sent)
(if (equal? 'um (first sent))
(+ 1 (count-ums1 (bf sent)))
(count-ums1 (bf sent))))
(define (count-ums3 sent)
(if (equal? 'um (first sent))
(+ 1 (count-ums2 (bf sent)))
(count-ums2 (bf sent))))
Write count-ums recursively.
11.3 [8.13]
Write a procedure phone-unspell that takes a spelled version of
a phone number, such as POPCORN, and returns the real phone number, in
this case 7672676. You will need a helper procedure that
translates a single letter into a digit:
(define (unspell-letter letter) (cond ((member? letter 'abc) 2) ((member? letter 'def) 3) ((member? letter 'ghi) 4) ((member? letter 'jkl) 5) ((member? letter 'mno) 6) ((member? letter 'prs) 7) ((member? letter 'tuv) 8) ((member? letter 'wxy) 9) (else 0)))
Here are some some special-case phone-unspell procedures:
(define (phone-unspell1 wd) (unspell-letter wd)) (define (phone-unspell2 wd) (word (unspell-letter (first wd)) (unspell-letter (first (bf wd))))) (define (phone-unspell3 wd) (word (unspell-letter (first wd)) (unspell-letter (first (bf wd))) (unspell-letter (first (bf (bf wd))))))
Write phone-unspell recursively.
Use recursion to solve these problems, not higher order functions (Chapter 8)!
11.4 Who first said "use what you have to get what you need"?
11.5 Write a procedure initials that takes a sentence as its
argument and returns a sentence of the first letters in each of the
sentence's words:
> (initials '(if i needed someone)) (I I N S)
11.6 Write a procedure countdown that works like this:
> (countdown 10) (10 9 8 7 6 5 4 3 2 1 BLASTOFF!) > (countdown 3) (3 2 1 BLASTOFF!)
11.7 Write a procedure copies that takes a number and a word as
arguments and returns a sentence containing that many copies of the given
word:
> (copies 8 'spam) (SPAM SPAM SPAM SPAM SPAM SPAM SPAM SPAM)
[2] It's a disease. Coal miners get it.
[3] As it happens,
there are no English words that start with more than four consonants.
(There are only a few even with four; "phthalate" is one, and some others
are people's names, such as "Schneider.") So we could solve the problem
without recursion by writing the specific procedures up to pigl4 and
then writing a five-way cond to choose the appropriate specific case.
But as you will see, it's easier to solve the more general case! A single
recursive procedure, which can handle even nonexistent words with hundreds of
initial consonants, is less effort than the conceptually simpler
four-consonant version.
[4] Exercise 8.12 in Part III asks you to solve this same problem using higher-order functions. Here we are asking you to use recursion. Whenever we pose the same problem in both parts, we'll cross-reference them in brackets as we did here. When you see the problem for the second time, you might want to consult your first solution for ideas.
Brian Harvey,
bh@cs.berkeley.edu